在与数学有关的游戏中，有一个历史非常悠久的问题，那就是研究国际象棋棋盘上马走过每个方格一次的路径。许多知名的数学家，如德莫弗（De Moivre）、欧拉（Euler）与范德蒙德（Vandermonde）等人，在过去的200年中都研究过这个问题，不过总还是会有新的发现。

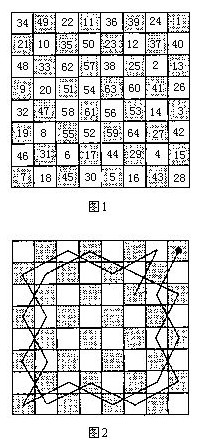
　　图1是德莫弗对8×8棋盘所作的一种解答，方格中的号码代表马的走法。图2是相同路径的另一种表示方法。两者各有其优点，你可以自行决定采用哪一种表示法。不论你使用哪一种方法，都会需要很多的方格纸。第二种使用直线连接的表示方法尚未完成，但已经显示出德莫弗解答的策略是，在棋盘上沿一个方向移动，而且尽可能地向外侧靠近。在方格纸上重新绘制图2，在自己尝试解题之前，先完成德莫弗的解。

　　对于这类问题，最好是从较小的棋盘开始，以便先熟悉马在各方格移动的方法。

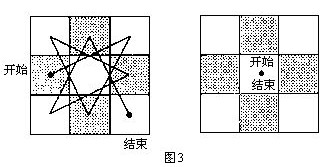
　　显然在3×3的棋盘上，马无法走完全程（图3）。从外圈的方格出发，马可以轻易地走过所有的外圈方格，但无法走到中央的方格；若是从中央的方格出发，马则无路可走。

　　那么在4×4的棋盘上，马是否可能走完全程？

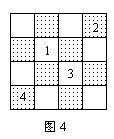
　　图4是个错误的走法，马走了4步之后就动弹不得。若你无法走遍所有16个方格，那么在不重复经过任一方格的情况下，最多能走过多少方格？

　　请研究马在5×5、6×6、7×7的棋盘上的路径。

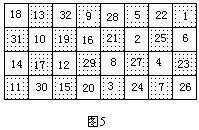
　　图5是马在8×4的长方形棋盘上的路径。马是否有可能在更小的长方形棋盘上走完全程？

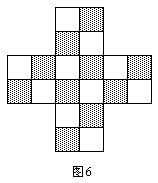
　　研究马在其他形状的棋盘上的路径也很有趣。如图6的形状，曾被作者误以为是不可能走完全程的形状，但其实是可以走完全程的。

　　言归正传，再回到传统正方形的棋盘。研究此问题的许多数学家都试图找出具有特殊性质的解，例如找出马最后回到起点的路径。

　　图7所示的走法由欧拉所完成。这种路径称为“重返路径”。图7的解还具有一种更奇妙的性质，那就是马先走完一半的棋盘，再走另一半。

　　请试着在6×6的棋盘上找出重返路径。

　　用一种很简单的方法可以证明，任何奇数方格的棋盘都不可能有重返路径。看看你能否找到这个证明方法。

　　在其他形状的棋盘上也可能找到重返路径。可试一试图9.另一种也是由欧拉所找出的解法，使许多其他人提出的解法相形见继。那就是马的路径可以形成8×8的幻方，即任何行或列（但不包含对角线）的数字和都等于260，如图8所示。试着去验算一下其“魔术般”的性质，并研究其路径的对称性。根据马的走法，也可以设计出一种有趣的游戏。从5×5的棋盘上的任一方格开始，两人轮流移动一个马。移动时不能重复已经走过的方格，走最后一步的人赢。