141．4×4幻方与高阶幻方 

　　在丢勒的幻方中，总和为34的其他4个数字包括：

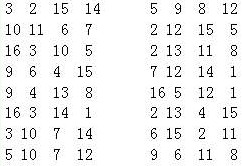
　　这种方阵曾被视为具有某种神秘的力量．

　　纳西克幻方不但包含了大部分丢勒方阵的对称性，而且还包括下列对角线形式的对称性，如：

142．多阶形式

　　3×3幻方所具有的性质恒为真，这可以由第140题“3×3幻方”解答中所给出的一般形式作代数证明．取任一常数k加至多阶形式的各数中，就能得出一个同次的新的多阶形式．

　　例如：

　　A+B+C+D=a+b+c+d

　　A²+B²+C²+D²=a²+b²+c²+d²则

　　(A+k)+(B+k)+(C+k)+(D+k)

　　=A+B+C+D+4k

　　=a+b+c+d+4k

　　=(a+k)+(b+k)+(c+k)+(d+k)

　　(A+k)²+(B+k)²+(C+k)²+(D+k)²

　　=A²+B²+C²+D²+2k(A+B+C+D)+4k²

　　=a²+b²+c²+d²+2k(a+b+c+d)+4k²

　　=(a+k)²+(b+k)²+(c+k)²+(d+k)²

143．帕斯卡三角形

　　帕斯卡三角形的下两行为：

　　除了1以外，其他数字都是由上一行中相邻的两个数字相加所形成的．每一行的数字和都是2的乘方；第十二行的总和为2¹¹=2048．

　　11的乘方

　　11的乘方至11⁴时，仍满足帕斯卡三角形的形式．11⁵由于会进位，所以并不能对应帕斯卡三角形第六行的数字1、5、10、10、5、1．

　　六边形迷宫

　　1 4 6 4 1

　　二项式

　　设a=1，看看帕斯卡三角形各行的数字和为何等于2的乘方．

　　把帕斯卡三角形的数字排成直角三角形，然后往上推，则显然也会出现(1+a)^-1与(1+a)^-2等的系数形式．

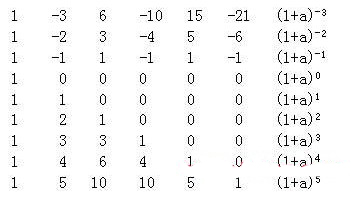
145．费波那契数列与黄金分割比

　　费波那契数列的规则可以用差分方程表示：

　　Uⁿ⁺²=Uⁿ⁺¹+Uⁿ

　　以两个1开始的此数列，各项的通式为：

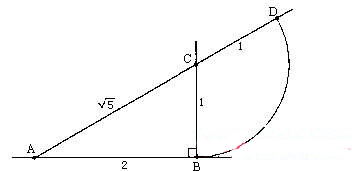
　　作出一个直角三角形，用圆规画出长为2的直线AB与长为1的直线BC，将A与C连线并延长．

　　以此类推．如果将得出的数组作向量，则其斜率就会趋近于黄金分割比．

146．称重问题

　　重量为1kg、3kg、9kg与27kg．用这4种法码就可称出所有1至40kg的整数重量．例如：

11=9+3-1 20=27+3-9-1

147．相似长方形

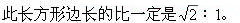
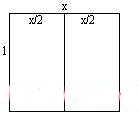
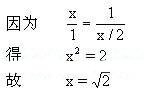
149．平衡问题

　　将球分成3堆，每堆9个球．先称其中两堆，如果天平平衡，则不合格的球必在另一堆；如果不平衡，则较重的9个球中必定包含不合格的球．不管是什么情况，称一次就能确定不合格的球在哪9个球中．再将这9个球分成3堆，每堆3个球，再称一次，就能确定不合格的球在哪3个球中．因此，只要再称一次，就能找出那只不合格的球．

　　另一个相当类似但却难得多的问题是：有13个球，其中有一个球与其他的12个球重量不同，但不知是较轻还是较重，请只称3次找出不同的球．